Introduction
Hello, and welcome to my small article about Quadratic Equations.
Quadratic Equations
In algebra, a quadratic equation is any equation in the form of ax2 + bx + c = 0. In the previous expression, x represents an unknown, and a, b, and c represent known numbers such that a is not equal to 0. The numbers a, b, and c are the coefficients of the equation, and can be distinguished by calling them the quadratic coefficient, the linear coefficient, and the constant or free term.
Our Project
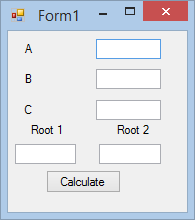
Use Visual Studio to create either a VB.NET or a C# Windows Forms Application and design the form to resemble Figure 1.
Figure 1: Design
Please note that my naming of objects may be different than yours.
Code
Add the following namespaces to your code:
C#
using System; using System.Windows.Forms;
VB.NET
Imports System.Math
Add the following fields to your form.
C#
private double sngCoEffA;
private double sngCoEffB;
private double sngCoEffC;
private double sngDiscriminant;
private double sngRoot1;
private double sngRoot2;
VB.NET
Private sngCoEffA As Double Private sngCoEffB As Double Private sngCoEffC As Double Private sngDiscriminant As Double Private sngRoot1 As Double Private sngRoot2 As Double
In the preceding code, you have created the Coefficient objects, Discriminant objects, as well as the Root objects. Add the following code for the Calculate button.
C#
private void btnCalculate_Click(object sender, EventArgs e)
{
sngCoEffA = float.Parse(txtCoEfficient1.Text.ToString());
sngCoEffB = float.Parse(txtCoEfficient2.Text.ToString());
sngCoEffC = float.Parse(txtCoEfficient3.Text.ToString());
sngDiscriminant = (sngCoEffB * sngCoEffB) - (4 * sngCoEffA
* sngCoEffC);
if ((sngDiscriminant > 0))
{
sngRoot1 = (-sngCoEffB + Math.Sqrt(sngDiscriminant)) /
(2 * sngCoEffA);
sngRoot2 = (-sngCoEffB - Math.Sqrt(sngDiscriminant)) /
(2 * sngCoEffA);
txtRoot1.Text = sngRoot1.ToString();
txtRoot2.Text = sngRoot2.ToString();
}
else if ((sngDiscriminant == 0))
{
sngRoot1 = (-sngCoEffB + Math.Sqrt(sngDiscriminant)) /
(2 * sngCoEffA);
MessageBox.Show("One Root");
txtRoot1.Text = sngRoot1.ToString();
}
else
{
MessageBox.Show("No Root");
}
}
VB.NET
Private Sub btnCalculate_Click(ByVal sender As System.Object, _
ByVal e As System.EventArgs) Handles btnCalculate.Click
sngCoEffA = txtCoEfficient1.Text
sngCoEffB = txtCoEfficient2.Text
sngCoEffC = txtCoEfficient3.Text
sngDiscriminant = (sngCoEffB * sngCoEffB) - (4 * sngCoEffA _
* sngCoEffC)
If (sngDiscriminant > 0) Then
sngRoot1 = (-sngCoEffB + Math.Sqrt(sngDiscriminant)) / _
(2 * sngCoEffA)
sngRoot2 = (-sngCoEffB - Math.Sqrt(sngDiscriminant)) / _
(2 * sngCoEffA)
txtRoot1.Text = sngRoot1
txtRoot2.Text = sngRoot2
ElseIf (sngDiscriminant = 0) Then
sngRoot1 = (-sngCoEffB + Math.Sqrt(sngDiscriminant)) / _
(2 * sngCoEffA)
MessageBox.Show("One Root")
txtRoot1.Text = sngRoot1
Else
MessageBox.Show("No Root")
End If
End Sub
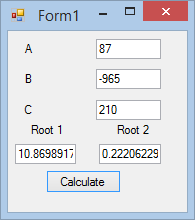
The code for the calculate button works out the Quadratic Equation based on the values that were input. When run, the Form might resemble Figure 2.
Figure 2: Running
Conclusion
Quadratic Equations might seem scary and daunting, especially when complicated formulas are involved. Hopefully, in a follow-up article I can explain a different technique. Until then, happy coding!